El simulador
Descripción del modelo
Existen diversas aproximaciones para modelar el crecimiento de bosques (Munro 1974; Weiskittel et al. 2011; Salas et al. 2016). Pellín adopta el enfoque de modelo de crecimiento de arbol individual independiente de la distancia. En esta sección se entregan antecedentes más específicos respecto a los componentes que integran al modelo de crecimiento implementado en Pellín.
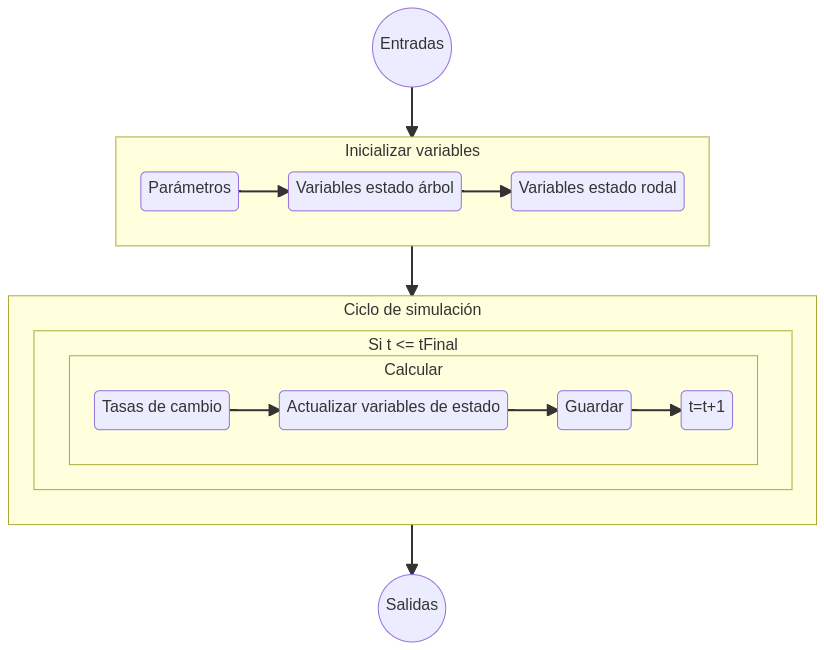
El diagrama de la figura 2 describe el flujo básico de un sistema de simulación de crecimiento forestal a nivel individual, como por ejemplo el de Pellín. Lo primero es leer los datos de control (lo cual se simplifica como Entradas en el diagrama), lo que corresponde no tan sólo a verificar el archivo con el listado de árboles, sino que también leer las definiciones para realizar la simulación, como lo son el horizonte de simulación y cargar los parámetros necesarios de los modelos internos a ser empleados. Luego de leidos estos datos de control, se inicializan las variables de estado a nivel de árbol y rodal, para el tiempo actual o inicial de simulación. Esto en términos computacionales equivale a una lista de información cuantitativa. El nucleo del simulador es el ciclo que iterativamente resuelve al sistema dinámico de ecuaciones que lo conforman. Dentro del ciclo de simulación, para cada variable de estado (tanto a nivel de árbol como de rodal), se calcula su nuevo valor en base a su tasa de cambio, y se actualiza el valor del listado de árboles. Posteriormente, se aumenta el lapso de tiempo \(\Delta t\), en el caso de Pellín igual a 1, y se inicia el ciclo nuevamente. Cuando el tiempo iguala al máximo estipulado de simulación, se detiene el proceso y se procede a generar las salidas.
 |
|---|
| Figura 2: Flujo básico de un sistema de simulación de crecimiento forestal a nivel individual como el de Pellín. |
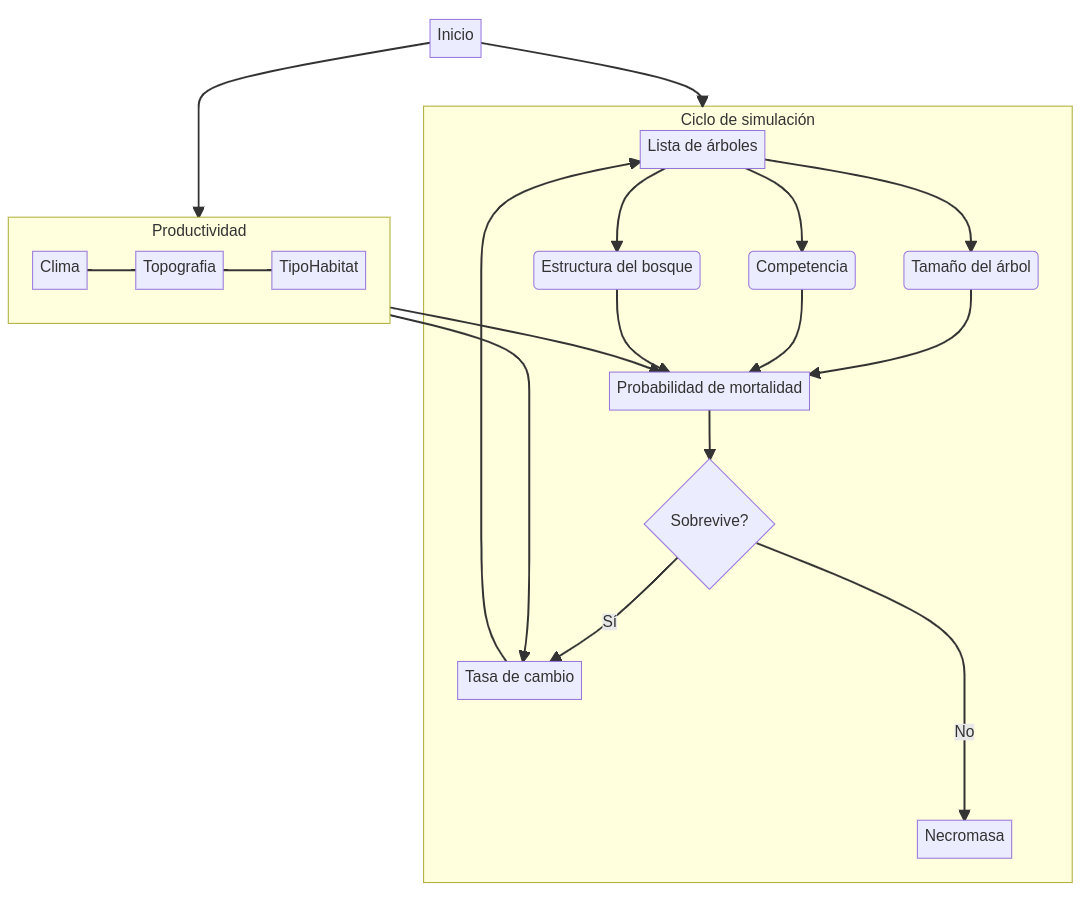
El flujo general del sistema de simulación Pellín se resume en la figura 3. El modelo de crecimiento a partir de las variables de tamaño de un bosque (i.e., lista de árboles), define la estructura de este, representandola mediante variables de rodal agregada y de orden, y variables que definen la competencia. Posteriormente, se calcula la probabilidad de mortalidad de cada individuo, y con los que sobreviven se predice sus respectivas tasas de cambio para el siguiente ciclo. De esta manera se genera una nueva lista de árboles que entra a un nuevo ciclo.
 |
|---|
| Figura 3: Flujo general del modelo de crecimiento de árbol individual del simulador Pellín. |
Documentos
Una característica importante para el equipo desarrollador ha sido el trabajo científico detras del modelo de crecimiento. Para esto, los autores han sometido a revisión de pares muchas de las ideas que sustentan a Pellín. Algunos trabajos donde se pueden revisar mayores detalles científicos en los cuales se basa el modelo son: Salas and Real (2013), Salas et al. (2016), Salas-Eljatib et al. (2018), Salas-Eljatib and Weiskittel (2018), Salas-Eljatib (2020), Salas-Eljatib and Weiskittel (2020), Salas-Eljatib (2021b), Salas-Eljatib (2021a), Salas-Eljatib et al. (2021). En la sección publicaciones aparecen los articulos, informes y otros documentos que sustentan el desarrollo del modelo de crecimiento implementado en Pellín.